I’ve been thinking a lot about how to do low-power computing systems, like around 10 mW (see Energy autonomous computing), and I think I have a handle on how to do a reasonable interactive computing environment in that energy budget. This note mostly focuses on prospects for fitting reasonable software into the hardware constraints of such low power. See Energy autonomous computing for details on other aspects of the issue.
I skimmed Bobrow’s 01966 “The Structure of a Lisp System using Two-Level Storage” the other day, and I was struck by his claim that BBN LISP was fast enough to be usable, even on an 18-bit PDP-1 (one of 53 ever made! And possibly the first!) with a 17–33 millisecond drum memory (5–10 μs per word sequential read) and a 16-kibiword core memory (5 μs per random word access, four times the standard size), even for 2–3 concurrent users. This is about half the speed of a Commodore 64 and only 36 KiB of RAM, but the drum was 88 kibiwords and much faster than a Commodore floppy. I thought I’d go back and read it in greater depth to see how this was possible.
Having read it, I think a number of modern techniques, particularly compressed oops, index registers, lexical scoping, bytecode, JIT compilation, and generational garbage collection, should make it possible to build a system with considerably more bang per computron than Bobrow had to settle for. Also, modern low-power microcontrollers have amounts of RAM comparable to the PDP-1’s, but are on the order of 1000 times faster, and have on the order of 1000 times more secondary storage available, which is about 100 times faster than the PDP-1’s; this should allow real, comfortable self-hosting microcontroller development. All of this can run on about ten milliwatts.
He allocated 4 KiW of core to compiled code (mostly in a 3400-word “ring buffer”), 4 KiW to the system (“supervisor and permanent code”, divided into six overlays), and the other 8 KiW to the stack and heap, and used two-word CONS cells. When paging a 256-word page of compiled Lisp in from the drum, the system linked (“relocated”) it.
It seems like the system could manage at most some 6000 calls per second:
Closed subroutine references to an in-core word through the [virtual memory page] map takes approximately 170 microseconds (because of the poor set of operation codes on the machine, and the lack of an index register).
Also, p. 16 (20/26) characterizes performance; it says that what we might now call the “cache hit rate” for RAM was about 97.5%, with only 2.5% of CAR and CDR operations going to the drum. This consumed only 10% of system time, presumably because all parts of the system were unbelievably slow: 31k CONSes and 150k CDR and CARs in 35 minutes, thus about 5000 of these operations per minute or 90 per second.
This seems to have been the paper that first published shallow binding (though in a strange way that uses pointers into the call stack), tagged pointers for small integers (“offset by 300,000 octal”, both positive and negative) and a form of BIBOP typing. I thought it also used CDR-coding, which I thought was the most interesting, but it doesn’t really.
The primary objective of the BIBOP typing was to avoid having to reach out to the drum for type tests, especially for symbols (where both of the usual predicates can be answered without waiting for a drum reference, namely ATOM and EQ) and so a contiguous chunk of the 17-bit (!) virtual address space was assigned to almost every type: value cells† starting at 0o150_000, property list cells†, full words (large integers), pushdown list (the call stack) starting at 0o200_000, function cells†, print-name pointers†, print-names, and “hash table”, which last runs from 0o270_000 (0x17000) to 0o300_000, although all of this this seems to conflict with the earlier statement that small ints from -32767 to +32767 were offset by 0o300_000, which would have them occupy the “address space” from 0o200_000 to 0o400_000. The virtual addresses from 0o10_000 to 0o150_000 are shared between “list structure” (shown growing down) and “compiled code” (shown growing up); although I have no idea how you would then distinguish a code pointer from a CONS, perhaps code pointers as such weren’t first-class values.
(A secondary benefit not mentioned is that CONS cells occupied two words instead of three, because they don’t need a type tag, but I guess devoting an entire word to type tags for dotted pairs was not considered as an option.)
He says this static allocation is preferred to “provid[ing] an in-core map of storage areas” because it reduces resident memory pressure (at the expense of virtual memory space efficiency). I suppose the 12 KiW of physical core being used for paging amounts to 48 pages, which is indeed pretty tight. If you divided the 17-bit address space up to 0o400_000 into “storage areas” of 0o4_000 homogeneous words, your type map would have 64 entries. If you could get by with a 3-bit type code for each “storage area”, you could squeeze 6 of them into each memory word; 4 per word would require 16 words of memory for the BIBOP map. They must have been pretty desperate to save 16 words of memory. But then, a static type allocation avoids writing code for dynamic allocation, too.
Above there are four items marked with “†”; these are the four virtual memory areas associated with symbols (“each literal atom”). Each is 0o10_000 in size, so I guess the system supported a maximum of 4096 symbols, and these were in essence parallel arrays. “A pointer to an atom* points to its value cell.” They’re separated in virtual memory because accesses to them tend to be not merely uncorrelated but actually negatively correlated — symbols used for functions tend not to be used for variables (“value cells”), almost nothing uses property lists, and print-name pointers are not normally used during actual computation. 4096 words is 16 256-word pages, so I guess you’d page in a sixteenth of the symbols’ value cells or function cells or whatever at a time.
* They did also consider numbers to be “atoms”, just not “literal atoms”.
Aha, here’s the resolution to the dilemma above about overlapping memory areas: although the call stack starts at 0o200_000, followed by function cells, print-name pointers, print names, and the hash table, none of these are first-class values! If you want to refer to a symbol, you point to its value cell, not its function cell or print name, so it’s totally kosher to use the addresses at 0o200_000 and up for small ints. Moreover the sequence simplifies some other type tests: anything over 0o150_000 was an “atom” (symbol or number), but anything over 0o170_000 was an integer, and anything over 0o200_000 was a small integer. So the boundaries were chosen with an eye to subset relations.
The “CDR-coding” didn’t actually use less space; the CDR pointers were
still fully materialized! It just attempted to maximize locality by
allocating (cons x y) on the first possible of y’s page, x’s
page, some page in core, or some swapped-out page. This used a
per-page free list and an in-core map of per-page free lists, which I
suppose must have used 192 words (!!) for the 49152 words of virtual
memory available for “list structure”.
They also mention an “additional scheme for dumping onto secondary storage (magnetic tape)” which I thought might have done the full CDR-coding thing, but it doesn’t seem to have done so. This is referenced to “Storage Management in LISP”, Bobrow, in preparation, Proc. IFIP Conf. on Symbol Manipulation Languages, and “A LISP Garbage Collector Algorithm Using Serial Secondary Storage”, Minsky, AIM-58, 01963.
Minsky’s paper seems to be scanned in full but with the page order
askew; it contains the longest program I’ve ever seen written in the
M-expression dialect of LISP, which is not very long at all: 27 lines
of code. It focuses on writing a sequence of (x, y, z) triples out
onto the drum, which, when read back in, put the dotted pair (y . z)
into register (memory location) x. So a linked list of 20 addresses
stored in the cars of 20 consecutive dotted pairs will need 60 words
on the drum, even more than in BBN LISP. Minsky comments:
Collect has the additional feature that all cdr sequences end up linearly packed! There are probably some important applications of this.
But I think compaction was his main focus, and I don't think of that as a hard problem, so I haven’t taken the time to grok collect in fullness.
An STM32F103C8 as used in a Blue Pill runs about 72 MIPS, 64 or usually 128 KiB of Flash, and 20 KiB of SRAM; the preassembled board costs about US$2. This chip uses about 1.5 nJ per 32-bit instruction (32.8 mA at 72 MHz, mostly one instruction per cycle, at 2.5 V, is 83 mW, or 1.1 nJ per clock cycle; but this is the datasheet’s max current consumption at 85° with all peripherals disabled; and lower voltages and higher clock speeds may be doable), and it can run ARM code from SRAM. But 20 KiB isn’t a lot of space, so you need some external memory.
As mentioned in Energy autonomous computing and Can you do direct digital synthesis (DDS) at over a gigahertz?, you can get a variety of memory chips to interface to the STM32; a rough outline of chips I think may be representative follows:
| read | write | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| type | Cost | ns/byte | nJ/byte | ns/byte | nJ/byte | bytes | nUS$/byte | GPIOs needed | |
| GD25D10C | 2SPI NOR | 30¢ | 50 | 0.4 | 27000 | 1800 | 512Ki | 4600 | 4? (SPI) |
| CY62136EV30 | SRAM | 111¢ | 45 | 6 | 45 | 6 | 256Ki | 4200 | 25? (parallel) |
| 23LC1024 | QSPI SRAM | 210¢ | 100 | 1 | 100 | 1 | 128Ki | 16000 | 4? (SPI; 6 if QSPI) |
| S34MS01G2 | SLC NAND | 100¢ | 45 | 1.2 | 160 | 4.4 | 128Mi | 7.5 | 15? (parallel NAND) |
| GD5F1GQ4 | QSPI NAND | 250¢ | 56 | 4 | 220 | 16 | 128Mi | 19 | 4? (SPI; 6 if QSPI) |
The parallel SRAM could actually be used in 16-bit-wide mode and get double the bandwidth and half the power usage, but use 7–8 more GPIO pins.
In theory it should be possible to gang up a bunch of SPI RAMs or SPI flash memories (of the same type!) and read from them in parallel, whether or not you can write to them in parallel. This would allow you to address them with a one-pin address bus.
NAND Flash must be read and written a page at a time — the two NAND chips profiled above use a 2048-byte page size. It’s very appealing as a form of secondary storage, especially for frequently-written data: the energy cost per byte written is lower than anything but a (volatile!) SPI SRAM, and the dollar cost per byte of capacity is about three orders of magnitude lower than the alternatives. The access latency doesn’t show up in the table, but it's on the order of 50–100 μs, which is nearly 1000 times slower than the 50–200 ns of the other memory types, coincidentally almost precisely in inverse proportion to the price per byte.
NAND also comes conveniently packaged with a ready-made FTL and SPI interface in the form of SD cards and MicroSD cards, but I imagine there might be power costs as well as the well-known reliability problems introduced by shitty FTLs.
Writing frequently-read data to a NOR Flash might actually save power as well, but this is an extreme measure: you'd have to read a given byte from NOR instead of the 23LC1024 SRAM 3000 times before paying for the cost of writing it into the NOR.
So, suppose we have a system consisting of an STM32F103C8 microcontroller, a 23LC1024 QSPI SRAM, and a GD5F1GQ4 QSPI NAND chip. When idle it’s using 20 μA at 2.5 V in the MCU, 4 μA at 2.5 V in the 23LC1024, and 90 μA at 1.8 V in the NAND unless we turn it off with a transistor — 162 μW for the Flash and another 60 μW for the rest of the system. A 2048-byte major page fault would initially take 114 μs at 72 mW in the Flash, working out to 8200 nJ, and about 34 μs at, I don’t know, 20 mA and 2.5 V in the MCU, so 50 mW and another 1700 nJ, total about 9900 nJ. At that point it’s occupying one of the 10 page slots in the MCU’s internal SRAM. Evicting that page to the SRAM (you might want to evict a subpage instead) would take another 200 μs and 10 000 nJ in the CPU, plus 2000 nJ in the SRAM, which brings up the very interesting point that low-power SPI SRAM stops being so low-power if it keeps the CPU busy longer!
(The above numbers may be too optimistic about the MCU; it’s more like 30 mA at full speed than 20 mA, according to the datasheet, though that’s the worst case at 85°.)
A tiny QSPI controller like the Raspberry Pi Pico’s “pioasm” coprocessors that allowed the CPU to page while continuing to compute would be super helpful. The STM32F103C8 does have a 7-channel DMA controller which can run its two hardware SPI peripherals, so that might actually be doable. The SPI peripherals support dual SPI but not quad SPI, so instead of 100 ns and 56 ns per byte, it would be 200 ns and 112 ns per byte, perhaps with correspondingly increased power usage in the peripherals — but you could power down the CPU or have it work on something else. This might increase the cost of major page faults to 16 μJ, with a latency of 150 μs, and decrease the cost of minor ones to 4 μJ, with a latency of 400 μs.
Paging out a dirty page to NAND would also take about 400 μs.
At this rate you could do 2500 minor page faults (plus evictions and pageouts) or 6700 major page faults per second, but the first would cost 10 mW and the second would cost 110 mW. 2500 page faults is about 20 times what you can do on spinning rust.
(Uh, but actually the SPIs on this MCU are only good up to 18 Mbit/s... maybe parallel memory isn’t such a bad option? Or a beefier chip?)
The STM32F103C8 mentioned above costs US$5 in the usual venues when it’s not out of stock, though evidently the Blue Pill makers have found cheaper chips. But 20 KiB of internal SRAM is small enough to be restrictive. What about bigger STM32F chips, or maybe an ESP32? The STM32F line goes up to 512KiB SRAM. Beefier chips might also help to speed up off-chip communication and thus get it over with faster, perhaps saving energy. To my surprise, many of them also use less power!
| Chip | SRAM size | Price | Power draw at 72MHz |
|---|---|---|---|
| STM32F103C8T6 | 20 KiB | US$5 | 30 mA? |
| STM32F410C8U6 | 32 KiB | US$3.50 | 8 mA? |
| STM32F401RCT6TR | 64 KiB | US$5.50 | 9 mA? |
| STM32F730V8T6 | 256 KiB | US$6 | 28 mA? |
| STM32F765IGT6 | 512 KiB | US$15 | 28 mA? |
| ATSAMG53N19B-AU | 96 KiB | US$1.50 | 7.2 mA (but only goes up to 48MHz) |
| CY9AF156NPMC-G-JNE2 | 64 KiB | US$2 | ⸘no datasheet‽ |
| M481ZE8AE | 64 KiB | US$2.50 | ⸘no datasheet‽ |
Some of these, like the STM32F730 and STM32F765, have built-in memory controllers designed to interface to external SRAM, SDRAM (!!), NOR Flash, and even NAND Flash.
See also Energy autonomous computing for notes on the Ambiq chips, which are both much lower power and have more RAM.
Suppose that we want to save the whole RAM state of the microcontroller in stable memory, like the NAND Flash, either because we want to shut the whole system down or because we want to switch to a totally different task. (Maybe we don’t even want to save, just reboot.) How expensive is that?
Using the STM32F103C8 and the S34MS01G2 numbers above, writing 20 KiB at 160 ns per byte and 4.4 nJ per byte is 3.2768 milliseconds and 90 μJ. Reading it at 45 ns per byte and 1.2 nJ is 900 μs and 24 μJ. The S34MS01G2 claims 10 μA “typical standby current”. The STM32F103C8 uses another 20 μA at idle (not “standby”! “Stop,” with the RTC.) So you can drop power usage by 95% by powering off the NAND but not the microcontroller. Saving the microcontroller’s state this way might cost 9 seconds of the NAND’s standby energy usage, or 3 minutes of the processor “stopped”, which is 3 milliseconds of running the processor flat out at 30 mW or so.
So it should be energy-affordable to checkpoint the microcontroller’s state this way on the order of 20 times per second during continuous computation, if that’s a useful thing to do. And it might make sense to cut power to the NAND when it’s okay for it to be unresponsive for a while — it claims to need 5 ms to get back to operational when you power it back on, and 3 ms to erase a page, so it might make sense to power it down with a MOSFET whenever it’s been idle for tens of milliseconds, thus cutting power use by a third and extending battery life by 50%.
When you’re handling 90wpm keystrokes, we’re talking about like 110 ms on average between keystrokes. If we need 48000 instructions per keystroke, which seems grossly excessive, that’s 1 millisecond of computation, so about a 1% duty cycle. This might add 500 μW of power usage, 50 μJ per keystroke, which is strikingly close to the cost of reloading the microcontroller’s entire state from the NAND! Still, it’s probably better to leave the NAND powered down most of the time.
The STM32F103C8 has a lower-power shutdown mode called, confusingly, “standby”, where it uses two or three μA instead of the 20 in the “stop” mode discussed above, which would extend idle battery life by a factor of 6–10. It’s harder to wake from, it takes 65 μs to wake instead of 5 μs, and the SRAM loses its contents, so if you go into standby mode you do have to reload the whole system from NAND or whatever. This seems reasonable for events like keystrokes where 6 ms is an acceptable response time, but still, rebooting could cost tens of microjoules if it involves reloading the full context. The 30 μW “stop mode” uses this much about once a second, so when keystrokes are coming in more frequently than that, it’s cheaper to just stop and not reboot for every keystroke.
For handling 1kHz mouse movements (125 Hz is a more typical mouse sampling rate) these deep power-down modes clearly don’t make sense.
The STM32L line includes microcontrollers like the STM32L011x3/4 with even lower power usage: 0.54 μA in “stop” mode rather than 20, and at full speed, 1950 μA at full speed (though that’s only 16 MHz) instead of 29000 μA. It might make sense to use a processor like this as a “supervisor” processor for the whole system, always on, and powering the other hardware up only when needed. That chip in particular has only 2KiB of SRAM, but to the extent that that’s sufficient for a user interaction, the rest of the system could remain turned off.
The 23LC1024 SRAM, if present, uses another 4 μA of standby current. It’s 128 KiB, so saving it to the NAND Flash (in preparation for unplugging it) would take almost 600 μJ and 21 ms at 4.4 nJ and 160 ns per byte. Leaving it unplugged for a minute (at 4 μA and 2.5 V) would pay back that energy cost, so unplugging it that way is only worthwhile when its idle time, or potential idle time, is up in the tens of seconds to minutes.
The upshot of all this is that it should be possible to reduce the system’s idle power consumption from some 35 μA (and nearly 100 μW) down to 20 μA with just the STM32F103C8, or down to 0.54 μA with an STM32L011, while keeping latency-to-full-responsiveness well under 10 ms. Even when actively editing text or browsing hypertext, it should be possible to stay below 500 μW, only leaping up to the full 83000 μW figure mentioned earlier when you’re actually computing something new, and maybe when you have the thing plugged in.
| Power store | 1 μW | 50 μW | 100 μW | 500 μW | 83000 μW |
|---|---|---|---|---|---|
| 2 J supercap | 23 days | 11 hours | 5 hours | 67 minutes | 24 seconds |
| 25 J pull on a pullstring | 10 months | 6 days | 3 days | 14 hours | 5 minutes |
| 2.2 kJ CR2032 coin cell | 70 years† | 17 months | 8 months | 7 weeks | 7 hours |
| 4250 mAh Li-ion 20700 (57 kJ) | 1800 years† | 36 years† | 18 years† | 43 months | 8 days |
| 2-kg 7Ah 12V lead-acid (300 kJ) | 9500 years† | 190 years† | 95 years† | 19 years† | 6 weeks |
† A CR2032 or 20700 only has a shelf life of about 10 years, so it will not last 18 years, much less 9500.
The NAND Flash discussed above is huge compared to everything else; the only penalty for bloated data representations in it is power usage and memory bandwidth usage. But for storing data in the microcontroller’s RAM, it’s crucial to represent it efficiently. Lisp data is pretty convenient to compute on but takes up a lotta fricking bytes.
What I originally thought when I skimmed Bobrow’s paper was that he was going to CDR-code lists in something like the following fashion. When some datum z produced by (cons x y) is placed on a page different from its cdr, it gets allocated a shortish buffer, with a counter and length packed into a word at its beginning:
|-----+---+---+---+---+---+---|
| 2/7 | y | x | - | - | - | - |
|-----+---+---+---+---+---+---|
If later we execute (let ((w (cons a z))) ...) the first thing we check is to see whether there’s more space available in z’s buffer. There is, so we stuff a into it:
|-----+---+---+---+---+---+---|
| 3/7 | y | x | a | - | - | - |
|-----+---+---+---+---+---+---|
Now, if we later cons something else onto w, like b, we may well be able to pack that into the same buffer:
|-----+---+---+---+---+---+---|
| 4/7 | y | x | a | b | - | - |
|-----+---+---+---+---+---+---|
Eventually the buffer gets full, or we try to cons two things onto the same thing, so then we allocate a new buffer, ideally on the same page. If the buffer got full we might want to allocate a bigger buffer.
This is all assuming there’s some sensible way to represent and dereference pointers into these buffers, and of course it would make RPLACD (set-cdr!) quite tricky.
With a buffer size of 8 words, like the above, we can store 6 cons cells in it, which would normally take 12 words, which is a best-case savings of 33%; as the buffer size grows, this approaches 50%. The worst-case inflation for 8 words is 4× (300%) but most lists are longer than that. The break-even point is at 4-item lists.
A quick Scheme program to count the lengths of lists, applied to itself, found 2 lists of length 0, 3 lists of length 1, 33 lists of length 2, 22 lists of length 3, 12 lists of length 4, and one list of length 5, which was the whole program and therefore possibly should not be counted. This is clearly not a fully representative sample of the data structures Lisp programs manipulate but it’s probably true that lists of length 2 and 3 are much more common than other lengths. (Also, none of the lists were improper.)
So, possibly a more optimal solution would be to use an initial buffer of size 4, and use a header bit to indicate whether the list is NIL-terminated or improper (or continued elsewhere). Then a 2-item list would be 4 words, the break-even point:
|---------+---+-------------+---+
| NIL/2/3 | 1 | delete-char | - |
|---------+---+-------------+---+
And a 3-item list would also be 4 words, a 33% saving over the standard approach:
|---------+-----+-----+--------------|
| NIL/3/3 | end | beg | make-overlay |
|---------+-----+-----+--------------|
If we initially allow such buffers (“obstacks”? “arenas”?) to extend to the end of their page, only capping them off at a bit over their current capacity when we want to allocate something else, we can reduce the number of spills. For example, consider parsing this Scheme into lists through recursive descent:
(define (freq-update vec n)
(let ((vec (vector-grow-init vec (1+ n) 0)))
(vector-set! vec n (1+ (vector-ref vec n)))
vec))
Here’s the conventional dotted-pair representation, as outlined for example in “A Command Structure for Complex Information Processing” from 01958 (p. 11, 13/54):
Each word is divided into two parts, a symbol and a link. ... The link is an address; if the link of a word a is the address of word b, then b is adjacent to a. That is, the link of a word in a simple list is the address of the next word in the list.
(See Some notes on IPL-VI, Lisp’s 01958 precursor for more notes on this amazing paper.)

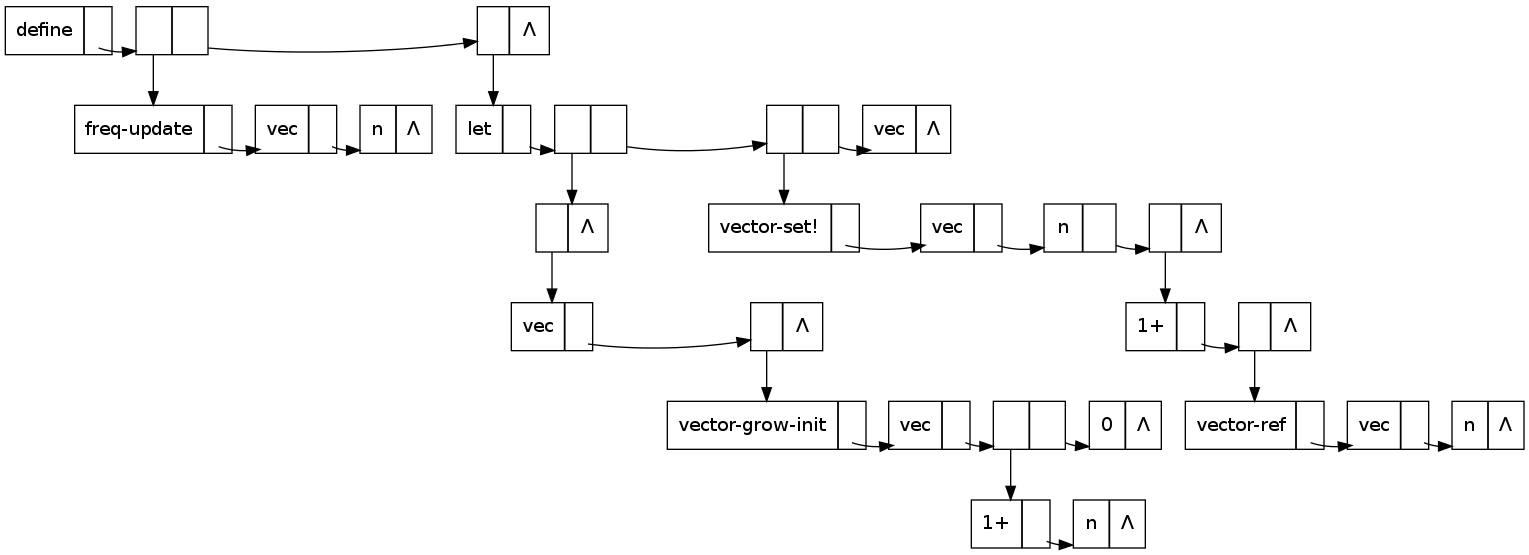
In Graphviz:
digraph fu {
node [shape=record, label="<car>|<cdr>"]
{
rank=same;
1 [label="define|<cdr>"];
1:cdr -> 2;
2:cdr -> 6;
6 [label="<car>|Λ"];
}
2:car -> 3;
{
rank=same;
3 [label="freq-update|<cdr>"];
4 [label="vec|<cdr>"];
5 [label="n|Λ"];
3:cdr -> 4;
4:cdr -> 5;
}
6:car -> 7;
{
rank=same;
7 [label="let|<cdr>"];
7:cdr -> 8;
8:cdr -> 10;
10:cdr -> 12;
12 [label="vec|Λ"];
}
8:car -> 9;
9 [label="<car>|Λ"];
9:car -> 13;
{
rank=same;
13 [label="vec|<cdr>"];
13:cdr -> 14;
14 [label="<car>|Λ"];
}
14:car -> 15;
{
rank=same;
15 [label="vector-grow-init|<cdr>"];
15:cdr -> 16;
16 [label="vec|<cdr>"];
16:cdr -> 17;
17:cdr -> 18;
18 [label="0|Λ"];
}
17:car -> 19;
{
rank=same;
19 [label="1+|<cdr>"];
19:cdr -> 20;
20 [label="n|Λ"];
}
10:car -> 21;
{
rank=same;
21 [label="vector-set!|<cdr>"];
21:cdr -> 22;
22 [label="vec|<cdr>"];
22:cdr -> 23;
23 [label="n|<cdr>"];
23:cdr -> 24;
24 [label="<car>|Λ"];
}
24:car -> 25;
{
rank=same;
25 [label="1+|<cdr>"];
25:cdr -> 26;
26 [label="<car>|Λ"];
}
26:car -> 27;
{
rank=same;
27 [label="vector-ref|<cdr>"];
27:cdr -> 28;
28 [label="vec|<cdr>"];
28:cdr -> 11;
11 [label="n|Λ"];
}
}
With recursive descent, the first cons we do is of vec onto '(),
creating a new buffer:
|-----------+-----+-----
| NIL/1/256 | vec | ...
|-----------+-----+-----
Then we start a totally new list by consing n onto '(), so we cap
off this one with a little room to grow and start a new one:
|---------+-----+---+-----------+---+-----
| NIL/1/2 | vec | - | NIL/1/252 | n | ...
|---------+-----+---+-----------+---+-----
Then we cons vec and vector-ref onto that:
|---------+-----+---+-----------+---+-----+------------+-----
| NIL/1/2 | vec | - | NIL/3/252 | n | vec | vector-ref | ...
|---------+-----+---+-----------+---+-----+------------+-----
Then we cap off that entire list and cons it onto '() followed by
1+:
|---------+-----+---+---------+---+-----+------------+---+---+-----------+----+----+-----
| NIL/1/2 | vec | - | NIL/3/5 | n | vec | vector-ref | - | - | NIL/2/246 | #6 | 1+ | ...
|---------+-----+---+---------+---+-----+------------+---+---+-----------+----+----+-----
So far we have 6 conses in 12 words, which is a singularly uninspiring performance.
A maybe more interesting representation of the above S-expression might annotate a flat list of atoms with their depths:
(define (freq-update vec n) (let ((vec (vector-grow-init vec ...
1 2 2 2 2 4 5 5
but of course this is not only just as many words of memory, it does not contain enough information to reconstruct the S-expression!
An RPN approach to reconstructing it might intersperse a series of N-ary operators on the symbol list:
1+ vector-ref vec n 3! 2! vec 4!
which at least compresses the six conses above down to 7 words instead of 12. For functions of fixed arity the N-ary operators are, strictly speaking, unnecessary — forward Polish notation is sufficient, so you could imagine representing that S-expression with the following whitespace-separated tokens:
define( freq-update vec n ){
let( vec vector-grow-init vec 1+ n 0 ){
vector-set! vec n 1+ vector-ref vec n
vec
}
}
That successfully represents the function code in 23 words, rather than 28 conses and thus 56 words, but at the cost of pushing most of the arity information into the symbols instead of the conses, which makes it quite awkward to compute with.
In the particular case that what you want to represent is something
analogous to Scheme source code, a structier approach may work better,
using ML-like pattern-matching and constructors, but Golang-like
slices for things like argument lists. That is, while you’re building
up an argument list, by all means use a cons list, but once you’re
done building it, freeze it into a counted array, which you can
comfortably cdr down with a slice. So, for example, let here takes
some variable-initializer pairs and some body expressions, in this
case one of the first and two of the second; and a function call takes
a function expression and some number of argument expressions.
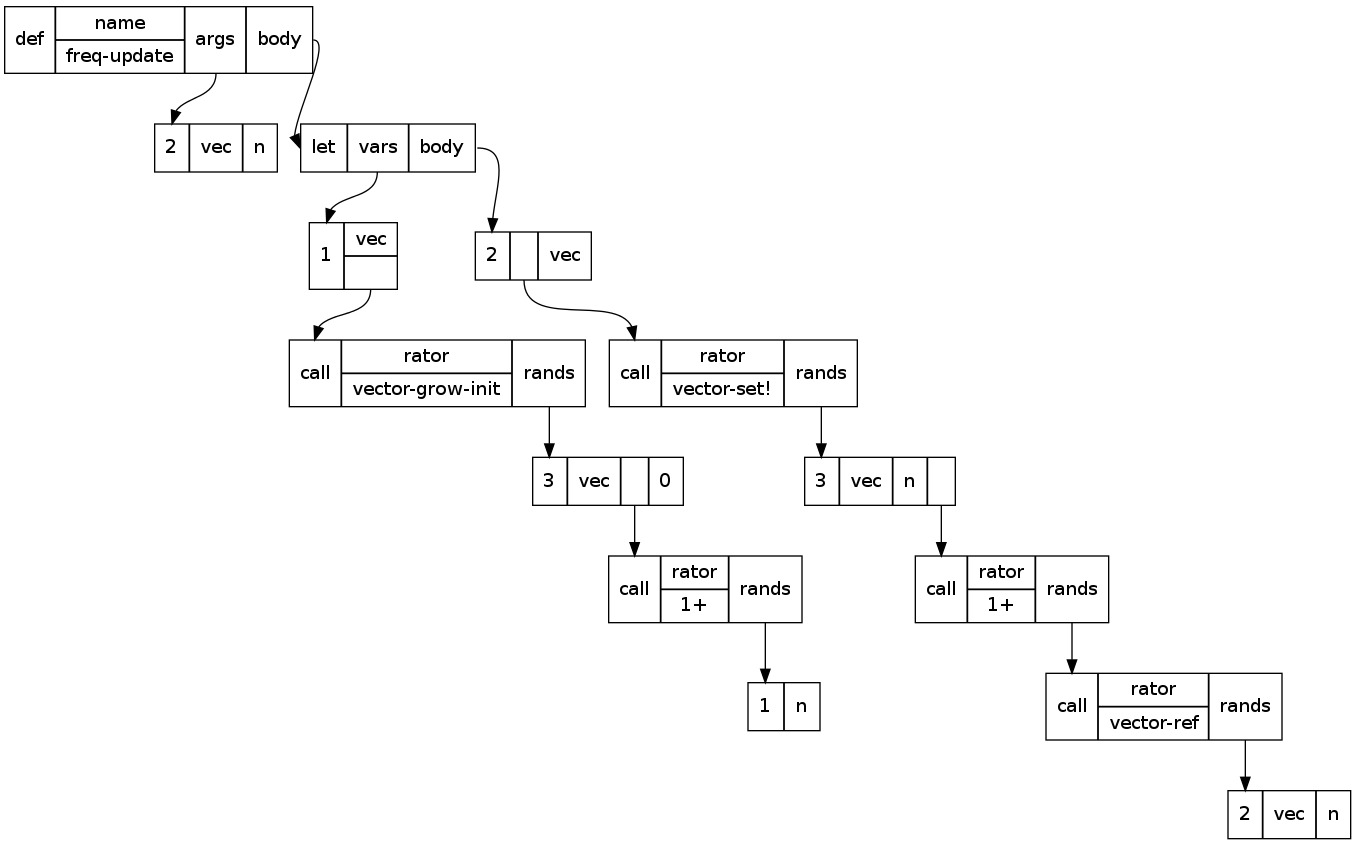
Here’s a thing that might look like in Graphviz:
digraph x {
node [shape=record]
func [label="<head>def|{name|freq-update}|<args>args|<body>body"]
func:args -> funcargs:head;
funcargs [label="<head>2|vec|n"]
func:body -> let:head;
let [label="<head>let|<vars>vars|<body>body"];
let:vars -> vars:head;
vars [label="<head>1|{vec|<init1>}"];
vars:init1 -> vecinit:head;
vecinit [label="<head>call|{rator|vector-grow-init}|<rands>rands"];
vecinit:rands -> vrands:head;
vrands [label="<head>3|vec|<incn>|0"]
vrands:incn -> incn:head;
incn [label="<head>call|{rator|1+}|<rands>rands"];
incn:rands -> incnrands:head;
incnrands [label="<head>1|n"];
let:body -> body:head;
body [label="<head>2|<1>|vec"];
body:1 -> x:head;
x [label="<head>call|{rator|vector-set!}|<rands>rands"];
x:rands -> y:head;
y [label="<head>3|vec|n|<z>"];
y:z -> z:head;
z [label="<head>call|{rator|1+}|<rands>rands"];
z:rands -> zz:head;
zz [label="<head>call|{rator|vector-ref}|<rands>rands"];
zz:rands-> zrands:head;
zrands [label="<head>2|vec|n"];
}
It looks better rendered with Graphviz dot, but Graph::Easy manages a crude ASCII-art rendition which I’ve cleaned up here:
+-----------------------------------------------------------------------+
| |
| +------+--------+--------------+-------+------+ +-----+------+-------+ +------+-----+----+
| | def | name | freq-update | args | body | --> | let | vars | body | | 2 | vec | n |
| +------+--------+--------------+-------+------+ +-----+------+-------+ +------+-----+----+
| | | ^
| | | |
v v v |
+----+-------+--------+ +------+------+----+ +-----+-------+--------+ +------------------+--------+-------------+-------+
| 2 | | vec | | 2 | vec | n | | 1 | vec | | | call | rator | vector-ref | rands |
+----+-------+--------+ +------+------+----+ +-----+-------+--------+ +------------------+--------+-------------+-------+
| | ^
| | +--------------------------------------------------------+
v v |
+------+--------+--------------+-------+ +-------+--------+-------------------+--------+ |
| call | rator | vector-set! | rands | | call | rator | vector-grow-init | rands | |
+------+--------+--------------+-------+ +-------+--------+-------------------+--------+ |
| | |
| | |
v v |
+------+--------+-----+-------+ +------+------+----+------+ +------+--------+--------+-------------------+--------+-------------+-------+-----+ |
| call | rator | 1+ | rands | | 3 | vec | n | | ----> | call | rator | 1+ | rands | 3 | vec | | 0 | |
+------+--------+-----+-------+ +------+------+----+------+ +------+--------+--------+-------------------+--------+-------------+-------+-----+ |
^ | | | |
| | | | |
| v | | |
| +------+--------+ | | |
| | 1 | n | +------------------------------------------+-------------+
| +------+--------+ |
| |
+-------------------------------------------------------------------------------------------------------------------------------------------------------------+
Here “rator”, “rands”, “vars”, and “body” are just field labels; they don’t occupy space on their own behalf, but they’re associated with pointers which do. The type-tags “def”, “let”, and “call” might possibly be able to be erased to some degree at runtime, or possibly handled in a BIBOP fashion. The “vars” of “let” are special in that the list is a list of 2-tuples, one of them in this case. If the type-tags are not erased, by my count this is 44 words of memory, which is better than 56 but still not great.
If we can erase the type-tags (but not the vector lengths), that drops us by 7 to 37 words. Also, in most cases, the vectors could be tacked onto the end of their parent record, eliminating a pointer, although this might conflict with type-tag erasure (since they’d be allocated within the same page as their parent record) as well as mutability (since this would necessitate copying them if another such record wanted to “reference” them, which would also be a possible solution to the erasure problem); the exceptions are func:args and let:vars. This reduces the space cost to 31 words.
(I notice one error in this diagram: the vector-ref call is being referenced directly from a rands field rather than by way of a 1-element vector. This makes 44 46, 37 39, and 31 32.)
32 memory words is 43% less space than 56. The ASCII Scheme version, which is inconvenient for computation, is 133 bytes, while 32 32-bit words is slightly smaller at 128 bytes — not counting the print-names of the symbols, which are shared with all of their other occurrences.
I think this sort of thing, inspired by ML ADTs, is likely to actually be more convenient for programming than S-expressions, as well as more space-efficient.
A possible BIBOP-alternative approach to handling type-tags, which still doesn’t require wasting an entire word in every object, is to store them on a separate page. Suppose we do embed the “rands” into call records, so their size depends on the number of arguments: two words if no arguments, three words if one argument, four words if two arguments, and so on; and suppose we use an allocator that allocates a page or subpage for each allocation size to prevent fragmentation (which of course conflicts with the locality-of-reference objective...). A 2048-byte page of 4-byte words has 512 words on it; if it’s divided into four-word objects, there will be 128 of them. Perhaps the memory allocator maintains a 128-bit bitmap of them elsewhere. Perhaps on a type-tag page there are 128 bytes that tell us the types of those 128 four-word objects: some may be two-argument calls, while others are single-expression-body lets, and others are single-expression-body defs. (This presumes that there are no more than 256 total type tags for four-word objects, and may lead to “read amplification” where we fault in an entire type-tag page even though 15 of the 16 pages it maps are swapped out.)
Probably a more reasonable approach is to dedicate pages to particular types of objects, such as calls, and subdivide them by size. So a 2048-byte page of calls might have 512 bytes (128 words, 64 objects) of two-word zero-argument calls; 512 bytes (42 objects) of three-word one-argument calls; 512 bytes (32 objects) of two-argument calls; and 512 bytes (25 objects) of three-argument calls. This allows you to minimize fragmentation and still do type-tests without faulting any pages in or limiting your number of types.
A different memory representation, much closer to the Lisp approach, would be to just replace lists with vectors. You can see that the Scheme code contains 10 lists and 19 atom references, for a total of 28 conses; here’s the code again:
(define (freq-update vec n)
(let ((vec (vector-grow-init vec (1+ n) 0)))
(vector-set! vec n (1+ (vector-ref vec n)))
vec))
(Or you can calculate it with this dumb code:
(define (atom-count sexp)
(cond ((null? sexp) 0)
((pair? sexp) (+ (atom-count (car sexp))
(atom-count (cdr sexp))))
(#t 1)))
(define (cons-count sexp)
(cond ((null? sexp) 0)
((pair? sexp) (+ 1
(cons-count (car sexp))
(cons-count (cdr sexp))))
(#t 0)))
(define (nil-count sexp)
(cond ((null? sexp) 1)
((pair? sexp) (+ (nil-count (car sexp))
(nil-count (cdr sexp))))
(#t 0)))
)
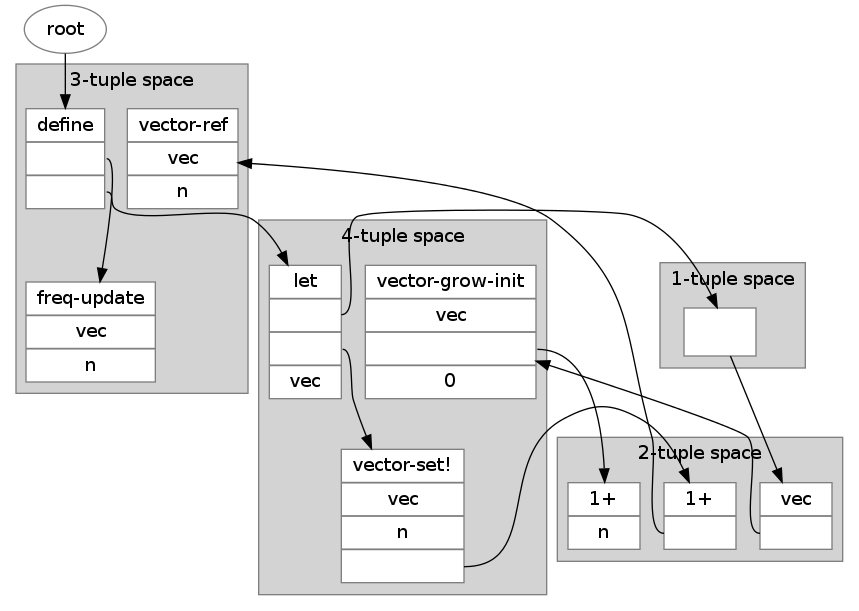
If you were to replace each list with a counted vector, these 28 conses in 10 lists would be only 38 words:
|---+-------------+-----+---+ +---+----+---|
| 3 | freq-update | vec | n | | 2 | 1+ | n |
|---+-------------+-----+---+ +---+----+---|
And if you were to segregate these vectors or tuples into pages or subpages by size, you could then omit the count fields (except on vectors too long to belong to a whole category of same-sized vectors, which would still need counts). Then instead of 38 words they would be 28 words. Optimal! All we had to sacrifice was mutability and tail sharing.
A Graphviz visualization looks like this:
digraph fu {
node [shape=record, style=filled, fillcolor=white, color="#7f7f7f"]
graph [style=filled, fillcolor=lightgrey, color="#7f7f7f"]
root [shape=oval];
root -> 6;
subgraph cluster_1 {
label="1-tuple space";
5 [label="<0>"];
}
subgraph cluster_2 {
label="2-tuple space";
2 [label="{1+|n}"];
4 [label="{vec|<1>}"];
9 [label="{1+|<1>}"];
}
subgraph cluster_3 {
label="3-tuple space";
1 [label="{freq-update|vec|n}"];
6 [label="{define|<1>|<2>}"];
10 [label="{vector-ref|vec|n}"];
}
subgraph cluster_4 {
label="4-tuple space";
3 [label="{vector-grow-init|vec|<2>|0}"];
7 [label="{let|<1>|<2>|vec}"];
8 [label="{vector-set!|vec|n|<3>}"];
}
3:2 -> 2;
4:1 -> 3;
5:0 -> 4;
6:1 -> 1;
6:2 -> 7;
7:1 -> 5;
7:2 -> 8;
8:3 -> 9;
9:1 -> 10;
}
An astonishing thing is that these 28 words are smaller than the 32 words taken up by the ML-like data structure outlined above, and under much less dubious assumptions.
This is clearly a broadly applicable data representation for things like syntax trees, binary search trees, and hash tables; and because you can do random access within the counted array it’s a reasonable structure for things like binary search and (non-in-place, because immutable) quicksort as well.
First, we could use ordinary pointers into the vectors as the iterator states. Unsafe cdr would then just be a pointer increment, but the null test would then require decoding the pointer’s bit representation and doing some kind of lookup to figure out what size the vector was, and maybe doing a modulo by the vector size (3 or 5 or something) to find the offset into the vector. This sounds like it would make cdring down a list spectacularly slow.
Second, we could use some kind of fat-pointer representation of iterators/ranges, like a base pointer and an offset, or an iterator pointer and an upper-bound pointer. CDR and NULL? are then fast but their argument no longer fits in a register; it needs two registers. (And, in the case of CDR, the result.) This has the additional advantage that you can efficiently refer to any range of a list, not just suffixes, and algorithms like binary search in the list also become more natural to express. With a Lua-like calling convention this isn’t necessarily a big practical problem for programming but it does add complexity, and you need list→iter and perhaps iter→list functions of some kind. list→iter in particular has to figure out how big the list is, through the kinds of pointer decoding and lookup that NULL? would have had to do in the previous option, but fortunately without the division operation.
Third, we could try to cram the fat-pointer representation into a single word somehow. For example, we could 8-byte-align all our vector pointers and use the three low-order bits to indicate an offset from 0 to 7, and chain together vectors to make lists of more than 8 items.
Fourth, we could maybe burst the vector into a conventional pile of dotted pairs when we start iterating over it, in some kind of very cheap garbage collection nursery or something. This obviously sacrifices mutability, which we already sort of did, but also damages EQ on lists, and it adds to the load on the GC.
Fifth, we could use a stateful generator coroutine, which is in some sense another version of “fat pointers”.
Incrementing a pointer in a loop, testing it against an end pointer, to do a linear search for a key, looks like this in reformatted GCC listing output for amd64, with the loop preamble removed:
25 0010 4883C708 .L8: addq $8, %rdi # increment pointer
27 0014 4839FE cmpq %rdi, %rsi # compare against end pointer
28 0017 7405 je .L2 # (fused with previous) exit loop
31 0019 483907 .L6: cmpq %rax, (%rdi) # compare against search key in %rax
32 001c 75F2 jne .L8 # loop while not found
33 .L2:
So it’s about 3–5 RISC instructions or micro-ops — and zero data memory accesses! — per loop iteration.
A context switch to a stateful generator coroutine can be as simple as an indirect jump or call, followed by another indirect jump or return later; but more generally you should expect to pay nearly the usual procedure entry/exit cost, because a lower cost would imply partitioning the register file between the generator and the consumer. Whatever registers the consumer clobbers aren’t available to maintain generator state, and whatever registers the generator clobbers aren’t available to maintain consumer state. The generator can keep its stack frame around from one yield to the next, but it still has to save any relevant callee-saved registers upon resuming and restore them on yielding, and vice versa for caller-saved registers.
Many lists — though few in the above example — are used as fixed-arity tuples rather than variable-length lists, and for these lists we’re probably most interested in pattern-matching them against patterns of the same arity, rather than iterating over their members. This is clearly much more efficient to do with these packed tuples than with linked lists of dotted pairs.
If you knew how many things are going to be in your output list, you could maybe preallocate it. MAPCAR, for example, could do this.
But the usual kind of Lisp code doesn’t know in advance how big a list it’s building, and knowing would make it more complicated. Consider this example (part of my solution to an exercise from Essentials of Programming Languages):
(define (set-subtract includes excludes)
(cond ((null? includes) '())
((member (car includes) excludes) (set-subtract (cdr includes) excludes))
(#t (cons (car includes) (set-subtract (cdr includes) excludes)))))
You could quibble with the crude coding style and the O(MN) algorithm, but I think it’s fair to say that writing recursive definitions of that sort and having them run with reasonable efficiency is a big part of the appeal of Lisp. But how do you write such a recurrence in this natural way, without losing the space-efficiency benefits of the packed vector representation?
One thing you could of course do is have a function that converts explicitly from the unpacked chain-of-dotted-pairs form into the packed form, and invoke it after the final recursive call:
(define (set-subtract includes excludes)
(list->packed
(let recur ((includes includes))
(cond ((null? includes) '())
((memb (ca includes) excludes) (recur (cd includes)))
(#t (cons (ca includes) (recur (cd includes))))))))
Exposing the difference to the user in this way would eliminate the
necessity for the ordinary functions car and at least cdr and so
on to handle both vector iterators (whatever their form) and
dotted-pair iterators, which might make them run faster. (However, if
they’re doing a run-time safety check, I think the extra cost to fall
back to a more general dispatch when the expected-type check fails is
probably insignificant.)
Alternatively, you could let the garbage collector take care of it:
when it copies a linked list of immutable dotted pairs out of the
nursery, it can count its length and copy it as a packed tuple into
the appropriate packed tuple bucket, instead of copying the dotted
pairs individually. This does require cdr to check which
representation is in use at any given moment, though. And sometimes
it’s important for both space and time to preserve some tail sharing
(though you can always restructure algorithms to do their sharing via
the car).
Such approaches were inconceivable before the invention of generational garbage collection in the mid-01980s.
(It might even be worthwhile to include the list length in the dotted pairs when you create them; although this fills up the nursery faster, it means the GC doesn’t have to pretraverse the list to count its length before packing it.)
As a third alternative you might consider explicit mutability:
def set_subtract(includes, excludes):
result = []
for item in includes:
if item not in excludes:
result.append(item)
return result
But this doesn’t really help with the problem at hand; CPython has to
preallocate a bunch of extra slack space for result, probably
several times, and the last time most of it never gets used. If you
say return tuple(result) you eliminate this space waste at the cost
of an extra copy, similar to the list->packed approach.
It sure is a lot less fucking code than the Scheme, though, isn’t it?
In this particular case an additional angle on the problem is to
consider set-subtract as a potentially lazy sequence transformer,
usable for example as a generator coroutine:
def set_subtract(includes, excludes):
for item in includes:
if item not in excludes:
yield item
If you want to materialize it, though, that still doesn’t help; the consumer of the generated sequence can do whatever they want with it, including packing it into a vector, but they don’t know in advance how big it is either!
The packed-tuple representations above eliminate tail sharing by duplicating the shared list tails, which is valid for immutable structures; the only question is whether it is more or less wasteful than representing the lists with materialized dotted pairs (in the words of “A Command Structure for Complex Information Processing” from 01958:
A list structure can be established in computer memory by associating with each word in memory an address that determines what word is adjacent to it, so far as all the operations of the computer are concerned. We pay the price in memory space of an additional address associated with each word, so that we can change the adjacency relation as quickly as we can change a word of memory.
One of the benefits of copying these shared tails is that it ensures that each list is on the same memory page as its tail, so no additional page faults are incurred in walking down the list. But this is not the only relevant locality criterion; we would also like the contents of the list to be on the same page, as BBN LISP’s allocation strategy attempts (see above about “CDR-coding”). With immutable list contents and the gigantic resources of NAND, we can achieve this to a significant extent by peremptorily copying immutable referents when we construct lists.
So far everything described has been described in terms of “words”, but I think the “Large Object-Oriented Memory” approach may be suitable for this kind of microcontroller system. Load and store instructions to internal SRAM on ARM Cortex-M3 microcontrollers commonly take 2 clock cycles, though sometimes this can be pipelined, so I’m guessing this would be 28 ns on the STM32F103C8 at 72 MHz, or 7 ns per byte. This is around 8–32 times faster than the access times to any of the other memories considered above, and consumes almost proportionally less energy, so avoiding off-chip access as much as possible would seem to be paramount.
The LOOM Smalltalk paper used 32-bit ordinary object pointers (“oops”) on disk, but 16-bit “compressed oops” in RAM. An in-RAM object table kept track of the correspondence. Such an approach could probably nearly double the effective capacity of the 20-KiB RAM on such a microcontroller. 20 KiB is enough to hold 20480 bytes, 10240 16-bit compressed oops, or 5120 32-bit oops or two-element vectors of 16-bit compressed oops. Moreover, for the NAND Flash sizes I was talking about above, you might want 40-bit or 48-bit uncompressed oops!
Even the largest low-power microcontrollers considered above have only 96 KiB of on-chip SRAM: 98304 bytes, 49152 compressed oops, 24576 dotted pairs or two-element vectors made of compressed oops, or 12288 32-bit oops. So clearly a 16-bit field is enough to address all the objects that will fit into SRAM at a time.
Compare these to the 4096 symbols and 0o140_000 = 49152 words devoted to compiled code and list structure in Bobrow’s paper: that’s also 24576 dotted pairs! But shared only with compiled code, not with symbols and integers and whatnot. We can take some comfort in being able to page things in 6000 times a second instead of 30 times a second — but in proportion to CPU speed this swapping rate is actually much slower. Bobrow’s 17-ms average rotational latency was only about 1000–2000 machine instructions, while 150 μs is about ten thousand instructions for our CPU. However, we can expect even much faster performance than that: Bobrow was only getting 6000 subroutine calls per second, about 15 instructions per call, which he attributes to the weaknesses of the PDP-1’s instruction set, but we ought to be able to get something like two or three times that amount.
LOOM supposedly paged objects in and out one at a time, but I can’t imagine that working very well for things like disk or NAND. Evicting individual objects would be fine for things like external SRAM, and faulting in individual objects would be fine for things like NOR.
You might also be able to use the compressed-oop approach advantageously within memory pages in NAND storage. With 40-bit uncompressed oops, a 2048-byte NAND page can contain only 409 pointers, or 204 dotted pairs, enough for a list of 204 things, or a counted vector of 408 things. Suppose that we allocate 1024 bytes of the page to a “link table” of 204 uncompressed oops, and the other 1024 bytes to 682 12-bit ultracompressed oops, organized into up to 682 tuples of various sizes, plus a little metadata. The 4096 slots in the 12-bit address space for these ultracompressed oops are divided among the 204 external pointers, the 682 or less internal objects, small integers, other popular objects like nil, and perhaps some objects cataloged on other “indirect pages”. We can still make a list of 204 external things, occupying a counted packed tuple in 206 of these 1024 bytes, but we can also represent quite complex data structures within this space. In a near-typical case where it’s entirely allocated to 3-item packed tuples mostly pointing within the page, the 409 uncompressed oops would have bought us 136 of them, but this compressed layout buys us 227 of them, a 67% increase in capacity, or from another point of view, a 40% decrease in the number of pages required. This 40% reduction in bulk reduces the number of page faults to fault in a given set of objects by some amount less than 40%, but that depends on the locality with which the objects are allocated: in the extreme case of no locality of reference, you still have one page fault per object, but in the extreme case of purely sequential access, you’d have a 40% reduction in page faults.
(Weirder representations are plausible too, like variable-size link tables and 10-bit ultracompressed oops; you could imagine, say, a page with 512 3-item packed tuples on it, packed 10 bits per ultracompressed oop, and a table of 25 uncompressed oops.)
Remember that faulting in this 2048-byte NAND page costs us around 10 μJ, which is worth around 7000 instructions at 1.5 nJ per instruction. We also another 10 nJ or so to write it back if we dirty it. So decreasing the number of pages needed by 40%, and the number of page faults by, say, 20%, is worth spending a fair number of instructions on decompression, though only 5 instructions or so per object.
In the microcontroller’s SRAM, it isn’t useful to try to maintain this ultracompressed representation, because the expense of maintaining three copies of each oop (uncompressed, ultracompressed, and 16-bit compressed) is greater than the savings from the ultracompressed version; moreover, the uncompressed oops are likely to be duplicated between pages in the working set.
By promiscuously duplicating immutable list structure onto such ultracompressed pages, we can both conserve their uncompressed-oop slots and improve locality of reference further; probably this is a very difficult problem to solve optimally, but admits robust heuristics that very frequently do much better than a totally naïve algorithm. Greedy depth-first packing, for example. This potentially also permits glomming objects together into a page in whatever order is convenient for paging things out, rather than along with whatever objects they previously shared a page with, thus perhaps improving the write-amplification problem common to all paging systems.
One variant of such an ultracompressed page containing the
freq-update definition used above as an example might look like this
in hex, using 8-bit indices instead of 12-bit for ease of reading and
understanding:
09 00 ; link table of 9 40-bit uncompressed oops
01 01 00 ; followed by one 1-tuple, starting at index 9
02 03 00 ; three 2-tuples, starting at index 0a
03 03 00 ; three 3-tuples, starting at index 0d
04 03 00 ; three 4-tuples, starting at index 10
00 ; and nothing else
f0 ad 55 27 ff ; uncompressed oop for symbol `define` (index 0)
20 ae 55 27 ff ; uncompressed oop for symbol `freq-update`
50 ae 55 27 ff ; vec
80 ae 55 27 ff ; n
b0 ae 55 27 ff ; vector-ref, index 4
e0 ae 55 27 ff ; let
80 b0 55 27 ff ; vector-grow-init
20 b1 55 27 ff ; vector-set!
b0 b1 55 27 ff ; 1+, index 8
0a ; 1-tuple at index 9 refers to first 2-tuple
02 10 ; 2-tuple at index 0a refers to symbol vec and first 4-tuple
08 0d ; 1+ and first 3-tuple
08 03 ; 1+ n, index 0c
04 02 03 ; first 3-tuple: vector-ref vec n
00 0f 11 ; second 3-tuple: define <last 3-tuple> <second 4-tuple>
01 02 03 ; last 3-tuple: freq-update vec n
06 02 0c f0 ; first 4-tuple: vector-grow-init vec <third 2-tuple> 0, index 10
05 09 12 02 ; let <1-tuple> <last 4-tuple> vec
07 02 03 0b ; vector-set! vec n <second 2-tuple>
If I haven’t screwed this up, this is a 15-byte header, a 45-byte link table of uncompressed oops, and 28 bytes of list structure, which would be 42 bytes in the 12-bit representation suggested above. 15+45+42 = 102 bytes, about 3.6 bytes per oop or per cons, 10 bytes per list, a number which should go down as the number of oops in a page rises from 28 up to 300–600. In SRAM the list structure might occupy 56 bytes of 16-bit compressed oops, if we’re content to forget about the origin of each packed tuple, but if not, we might need an additional 50-byte-or-more chunk of the in-SRAM uncompressed oop table to remember where each of these 10 vectors came from.
This last consideration suggests that such compressed pages should list not only outgoing references in a link table, but also “labels” for incoming references. The idea is that labeled objects in the compressed page would be assigned an uncompressed oop so they could be referenced from outside the page, while unlabeled objects (necessarily immutable) can only be copied, not referenced. This might also allow us to use multi-gigabyte Flash effectively with uncompressed oops weighing only 32 bits rather than 40.
Consider a 256-gibibyte SD card, containing 2³⁸ bytes, which is currently near the ceiling for what’s easily available as an SD card (though 512 gibibytes isn’t unheard of, even 256 gibibytes costs US$40, 32 gibibytes is more common at around US$5, and 16 gibibytes is now under US$3 at retail). If our uncompressed oops were only 32 bits, the average object size would have to be 64 bytes, which is too big for cons cells or 3-tuples. If it’s divided into 2048-byte pages, it has 2²⁷ pages; 32-bit uncompressed oops would give us 32 labels per page. (You might want some kind of extra layer of indirection somewhere so that the oop numbers don’t directly give you physical block numbers, though). It’s easily plausible that you could get down to 32 externally-referenced atoms or chunks of list structure per 2048-byte page.
Bobrow doesn’t mention bytecode at all. Given the killer advantages of bytecode for what he’s doing, this surprised me, but apparently compiling to bytecode interpreters started with Wirth and Weber’s EULER in 01965, where it was presented not as a hack to reduce memory usage but an alternative to the λ-calculus for formally defining programming-language semantics, so it wasn’t a well-known technique at the time (p. 56):
The definition of the compiling system consists of the parsing algorithm, given in paragraph III.B.1., a set of syntactic rules, and a set of corresponding interpretation rules by which an EULER text is transformed into a polish string. The definition of the executing system consists of a basic interpreting mechanism with a rule to interpret each symbol in the polish string.
Where introduced, the “bytecode” in question didn’t have a defined
representation as a sequence of bits or numbers, so it’s maybe okay to
call it “p-code” but not than “bytecode”; however, the appendices of
the TR do include a full program listing in Burroughs B5500 Extended
Algol, evidently written by Wirth and Bill McKeeman† in 01964 and
01965. Stanford’s scan is badly corrupted, and I’m not sure my
understanding is entirely correct, but it doesn’t seem to try to pack
operands into bytecode bytes, or indeed even pack operators into
single bytes. (The family resemblance to the current Oberon compiler
is remarkably close!) I may be misunderstanding something but it
looks like the “bytecode” was actually an array of records named
PROGRAM with record fields named AFIELD, BFIELD and CFIELD.
BFIELD was used for “immediate operands” for loading numbers and
symbols onto the stack. These seem to be defined as follows, making
me think they may be bitfields in the B5500’s 48-bit words:
DEFINE AFIELD=[39:9]#,BFIELD=[9:30]#,CFIELD=[1:8]#;
So, as implemented, it wasn’t so much a bytecode as a “wordcode”.
However, Zork, old versions of Multiplan and Excel (especially on the Macintosh), GNU Emacs, and Smalltalk systems get a lot of mileage out of bytecode virtual machines, which allow them to squeeze a lot more code into very small computers than you would think possible. This command from my .emacs is 16 lines of code, but it compiles to 44 bytes of Elisp bytecode, plus some tables of constants and external references (literals, symbols):
(defun markdown-tt-word ()
"Hit N times to enclose previous N chunks of nonwhitespace in `` (for Markdown)."
(interactive)
(if (looking-back "`")
(save-excursion
(backward-char)
(search-backward "`")
(delete-char 1)
;; (backward-word) previously
(search-backward-regexp "\\S-")
(search-backward-regexp "\\s-")
(forward-char)
(insert "`"))
(progn
(insert "`")
(save-excursion
(backward-word) ; should this use the same simpler approach?
(insert "`")))))
I think it’s atypically dense to get just 3 bytes of bytecode per line of code; 6 bytes per line is probably closer.
Here’s a disassembly of the 44 bytes. You can see that they use a
stack bytecode with a single operand — usually packed into the same
byte, much like Smalltalk bytecode, but in the case of goto-if-nil
it seems to have a two-byte immediate operand following the bytecode.
The operands packed into constant and varref bytecodes are indexes
into pools of such things, again as in Smalltalk. Specific opcodes
are allocated to popular Emacs operations like save-excursion,
forward-char, and forward-word.
byte code for markdown-tt-word:
args: nil
interactive: nil
0 constant looking-back
1 constant "`"
2 call 1
3 goto-if-nil 1
6 save-excursion
7 constant -1
8 forward-char
9 discard
10 constant search-backward
11 constant "`"
12 call 1
13 discard
14 constant delete-char
15 constant 1
16 call 1
17 discard
18 constant search-backward-regexp
19 constant "\\S-"
20 call 1
21 discard
22 constant search-backward-regexp
23 constant "\\s-"
24 call 1
25 discard
26 constant nil
27 forward-char
28 discard
29 constant "`"
30 insert
31 unbind 1
32 return
33:1 constant "`"
34 insert
35 discard
36 save-excursion
37 constant -1
38 forward-word
39 discard
40 constant "`"
41 insert
42 unbind 1
43 return
Let’s see how our example code from earlier fares:
(define (freq-update vec n)
(let ((vec (vector-grow-init vec (1+ n) 0)))
(vector-set! vec n (1+ (vector-ref vec n)))
vec))
In Elisp that’s spelled:
(defun freq-update (vec n)
(let ((vec (vector-grow-init vec (1+ n) 0)))
(aset vec n (1+ (aref vec n)))
vec))
Emacs compiles the code part of this to 18 bytes of bytecode, 4½ per line; this is a lot less than 28 compressed oops (56 bytes).
byte code for freq-update:
args: (vec n)
0 constant vector-grow-init
1 varref vec
2 varref n
3 add1
4 constant 0
5 call 3
6 dup
7 varbind vec
8 varref n
9 varref vec
10 varref n
11 aref
12 add1
13 aset
14 discard
15 varref vec
16 unbind 1
17 return
It’s a little bit unfair not to count the argument list and constants
vector here, because they allow the references to vec and n and
vector-grow-init to fit into a few bits of a byte, while normally
they would require 8 bytes, as the elements of the argument list and
constants vector do. Only a little unfair, though.
It is surely not at all coincidental that the ultracompressed-oop stuff in the previous section looks very much like this bytecode structure. The argument list and constants vector are very similar to the “link table” for a page, but the link table is shared among the several hundred ultracompressed oops on that page, rather than just the several dozen bytecodes of an Emacs function.
There exists previous work on this. PICBIT was a bytecoded Scheme for PIC microcontrollers, but its bytecode was an order of magnitude fatter than the 6 bytes per line of code I suggested above; it was a successor to the slimmer BIT, which fit the R4RS Scheme library into under 8000 bytes of bytecode.
Immutable list structure can be productively represented by a sort
of bytecode as well, but this probably isn’t worthwhile. Given the
same “link table” vector of 9 atoms as above in the section on
“compressed oops in secondary storage”, in Elisp notation [define
freq-update vec n vector-ref let vector-grow-init vector-set! 1+], we
could represent our example Scheme definition as the 39-byte string
“(0(123)(5((2(62(83)@)))(723(8(423)))2))”. Here “(” is the “nest”
bytecode, “)” is the “nil” bytecode which terminates a list, the ASCII
digits are indices into the link table, and “@” is the small-integer
0; pointers into the list structure are represented by pointers before
its bytes. null? is straightforward (is a pointer pointing before a
“)”?) and car either decodes the byte following the pointer or, in
the case of “(“, returns an incremented pointer, which is the same
distinction atom? must make. Only cdr is tricky, since it must
increment the pointer past either an atom or an arbitrary-length list.
A table of minimal nesting depth per 8-byte chunk would probably make
this adequately efficient by enabling cdr to rapidly skip over
large, deeply-nested chunks:
(0(123)( 0
5((2(62( 2
83)@)))( 2
723(8(42 2
3)))2)) 1
You could assign better bytes, but this is probably not worthwhile. Not counting the link table, this bytecoded list structure uses 39 bytes (as opposed to the 18 bytecode bytes for the compiled code), 44 including the skip table, while in its packed-tuple form it occupies only 28 oops: 56 bytes in the 16-bit case, 42 bytes in the 12-bit case. If we were to use 8-bit compressed oops (as the above bytecode implicitly does), limiting the bytecode to only 256 referents, they would be 28 bytes, which is less than 39. Also, the packed tuples are more efficient to traverse and can support mutation.
It probably is worthwhile to burn large amounts of bytecode into the microcontroller’s Flash and interpret it from Flash; that way you don’t have to spend precious RAM on code. (128 KiB would hold about 20,000 lines of high-level code by the above estimate — the whole VPRI STEPS complexity budget — but of course the system has to use some memory too.) It’s probably okay for loading a new application to take a good fraction of a second if that frees up RAM for data. Most modern microcontrollers support pagewise reprogramming of their internal (NOR, painfully slow) Flash during operation, so this kind of thing should be acceptable even for exploratory interactive development.
† McKeeman also evidently invented peephole optimization in 01965, differential testing in 01998, and was Hehner’s advisor’s advisor, but he wasn’t credited in the TR.
In a memory-constrained environment, it’s surely worthwhile to compile all code to bytecode like the above, rather than interpreting directly from dotted pairs as BBN LISP did (or from packed tuples). Compiling into machine code is a more dubious proposition, since machine code tends to be much bulkier than bytecode, but the typical interpretive slowdown is a factor of 10–40, which in this case could translate to 10–40 times shorter battery life for compute-bound tasks.
Ur-Scheme uses a very simple and dumb compilation scheme (the same one as Bigforth, the one Crenshaw uses in “Let’s Make a Compiler”) for expressions, and open-codes the common cases of built-in operations, preceded by a dynamic type check (typically provided by “millicode”, though I didn't know the name at the time). The consequence is that it compiles its own 1553 lines of Scheme into 90168 bytes of i386 code (plus 45K of data, mostly read-only), almost 60 bytes of machine code per source line, doing things like this:
call *%ebx
pop %eax
push %eax
movl $2 + 256<<2, %eax # Ur-Scheme’s representation of nil
.section .rodata
# align pointers so they end in binary 00
.align 4
_parse_eofP_9: # in-memory read-only representation of string
.long 0xbabb1e
.long 3
.ascii " ()"
.text
push %eax
movl $_parse_eofP_9, %eax
# get procedure
push %eax
movl (_parse_string_1), %eax
# apply procedure
call ensure_procedure
movl 4(%eax), %ebx
movl $1, %edx # argument count
call *%ebx
# get procedure
push %eax
movl (_emit_malloc_n_4), %eax
This compiles to something like the following:
805d9f4: ff d3 call *%ebx
805d9f6: 58 pop %eax
805d9f7: 50 push %eax
805d9f8: b8 02 04 00 00 mov $0x402,%eax
805d9fd: 50 push %eax
805d9fe: b8 48 2f 06 08 mov $0x8062f48,%eax
805da03: 50 push %eax
805da04: a1 74 95 06 08 mov 0x8069574,%eax
805da09: e8 58 a7 fe ff call 8048166 <ensure_procedure>
805da0e: 8b 58 04 mov 0x4(%eax),%ebx
805da11: ba 01 00 00 00 mov $0x1,%edx
805da16: ff d3 call *%ebx
805da18: 50 push %eax
805da19: a1 24 94 06 08 mov 0x8069424,%eax
These 40 bytes of machine code in 14 instructions (one invoking a millicode routine) are part of the compilation results from this line of code, which invokes no macros:
(assert-equal (parse-string " ()") '())
It’s easy to do a little better than this with peephole optimization, but I think doing much better requires not just register allocation (at least in an extremely stupid form) but also some kind of static type system so we can avoid the endless type tests. I mean you could imagine the above getting compiled to the following:
movl $_parse_eofP_9, %eax # load string pointer
call _parse_string_2
xor %ecx, %ecx # load nil
And that would be 12 bytes instead of 40, and 3 instructions instead
of 14 (plus the 5 instructions in ensure_procedure). But for that
you’d have to know statically that parse-string was a procedure (and
not a closure or, say, an integer) and that it took one argument. To
avoid additional redundant checks inside of it, you’d also need to
know that that argument was a string.
By contrast, the source code would be four oops of list structure, and it compiles to 4 bytes of Elisp bytecode out of these 7:
byte code for test-assert-equal-parse-string:
args: nil
0 constant assert-equal
1 constant parse-string
2 constant " ()"
3 call 1
4 constant nil
5 call 2
6 return
As a very crude sort of estimate:
| form | weight |
|---|---|
| unoptimized i386 code | 40 bytes |
| source text | 25 bytes |
| dotted pairs, 16 bit | 16 bytes |
| optimized i386 code | 12 bytes |
| packed tuples, 16 bit | 8 bytes |
| packed tuples, 12 bit | 6 bytes |
| bytecode | 4 bytes (plus constant vectors, etc.) |
I haven’t tried it on ARM or RISC-V but I think the results will probably be about the same as i386, maybe a bit smaller. So we should expect easily generated machine code to be around 4 times the size of the list-structure source code, reasonable machine code to be about the same size as the source code, and bytecode to be smaller than that by a factor of 2–4.
When compiled with itself, Ur-Scheme, despite the slowdown factor of 4–8 evident in the above code, executes only 678,737,113 userland instructions to compile itself a second time (180 ms, only ⅔ in userland), about 437 instructions per line of source code. The executable contains 29355 instructions, so generating each output instruction takes about 23 instructions. Presumably it would be about 30 kilobytes of code and 8000 instructions, and need to run about 128 instructions per source line, if it were compiled with a decent compiler — but also generate a smaller amount of output code, so the 23-instruction ratio stays the same. Being such a decent compiler might slow it back down to 512 instructions per source line or, say, 128 instructions per output instruction. (Then again, it might speed it up.)
This suggests that, when you can execute from RAM, the iteration count at which a JIT compilation pays off timewise is on the order of 4–32. If you have a straight-line chunk of bytecode that can be JIT-compiled to a sequence of 32 instructions, then doing that compilation (at 128 compiler instructions per output instruction) might cost you 4096 instructions. Each time you interpret the bytecode at an interpretation slowdown of 16×, you spend 512 instructions on interpretation, so after 8 repetitions you’ve wasted the 4096 instructions you could have used on compiling it. If it’s possible to cut the compilation time down to 24 compiler instructions executed per compiled instruction output, then the breakeven point is 1½ iterations!
So, particularly if decent static type information is available, you’d get a pretty good reduction in battery usage by compiling most bytecode to machine code, even if you had to discard the compiled machine code after a small number of executions. It might even be worthwhile to always JIT-compile the bytecode. This approach, in turn, reduces the pressure on bytecode to be fast to unpack, so you can use bytecode representations that require more computation to understand, enabling you to fit more bytecode in RAM at once. For example, you could use variable-length instruction and operand encodings.
Compiled machine code that is executed many times is a good candidate for promotion to the microcontroller’s flash to free up RAM. Since this is NOR, we can expect to pay on the order of 2000 nJ per byte to erase and program it, so “many times” means something on the order of 4096 = 2¹² times — but perhaps it should also outweigh whatever compiled code must be evicted to make room for it, since we can only erase and reprogram Flash pages 100k ≈ 2¹⁷ times or so. Otherwise we are going to wear out a Flash that can hold 2¹⁶ instructions after something like 212+17+16 = 2⁴⁵ instruction executions. That’s about an hour.